El análisis de la deducción se centra en el establecimiento de las conexiones encadenadas por medio de la cópula “es”. Un argumento categórico está constituido por dos premisas y una conclusión en la que se establece una nueva conexión a través del término medio. La premisa que contiene el sujeto de la conclusión es la premisa menor y la que lleva al predicado, es la mayor. En la estructura se presenta:

También contienen enunciados de cantidad (UNIVERSAL -> todos, ninguno; PARTICULAR -> algún, algunos) y de polaridad (afirmativa o negativa) dando lugar a cuatro tipos de proposiciones: universal afirmativa, universal negativa, particular afirmativa o particular negativa.
- UNIVERSAL afirmativa (A) Todos los A son B;
- UNIVERSAL negativa: (I) Ningún A es B; No todos los A son B;
- particular afirmativa: (E) Algún A es B.
- particular negativa: (O) Algunos A no son B;
También hay que tener en cuenta la posición del término medio (B) en cada una de las premisas.
Existen cuatro posiciones que dan lugar a cuatro figuras del silogismo:
| Figura 1 | Figura 2 | Figura 3 | Figura 4 |
|
B A C B C A |
A B C B C A |
B A B C C A |
A B B C C A |
|
Es la más utilizada, la más fácil de general |
Se dan 256 silogismos posibles de la combinación de los cuatro enunciados en las dos premisas y la conclusión y en las cuatro figuras. Pero de todos ellos, solo 24 silogísmos categóricos son válidos. Silogismos válidos con conclusiones fuertes y débiles (24):
| Figura 1 | AAA | AAI | AII | EAE | EAO | EIO |
Ejemplo de AAI: Primera premisa A (universal afirmativa): Todos... son... Segunda premisa A (universal afirmativa): Todos... son... Conclusión I (particular afirmativa): Algunos... son... |
| Figura 2 | AEE | AEO | AOO | EAE | EAO | EIO | |
| Figura 3 | AAI | AII | EAI | EIO | IAI | OAO | |
| Figura 4 | AAI | AEE | AEO | EAO | EIO | IAI |
Hay que señalar que el no total de silogismos válidos incluye todas las conclusiones válidas, sean fuertes o débiles. Una débil será aquella que se obtenga como conclusión particular, cuando se permite una conclusión universal. Por ejemplo, un AAA sería:
| Figura 1 | Modo AAA | |
|
B A C B C A |
Todos los hombres prudentes evitan el tabaco Todos los médicos son hombres prudentes Todos los médicos evitan el tabaco |
A A A |
Es un silogismo válido fuerte AAA como figura 1 y con conclusión A. Pero podríamos decir: Algunos médicos evitan el tabaco (I).
Podemos ver que la conclusión fuerte sería la universal afirmativa (A) pero existe posibilidad de concluir con una débil, así considerada por existir la posibilidad dentro de esa figura de la AAA.
Algunos autores no hacen esta diferencia y solo consideran las conclusiones fuertes y el número de silogismos válidos, siendo 19 los considerados:
| Figura 1 | AAA | AII | EAE | EIO | ||
| Figura 2 | AEE | AOO | EAE | EIO | ||
| Figura 3 | AAI | AII | EAI | EIO | IAI | OAO |
| Figura 4 | AAI | AEE | EAO | EIO | IAI |
En un estudio que hizo Johnson -Laird y Steedman (1978) se encuentra que no siempre se considera la segunda premisa como sujeto de la conclusión, produciéndose conclusiones en ambos sentidos -> C A (que sería lo que se supone sería la forma de cualquier conclusión en cualquier figura, por eso todos la tienen así en el cuadro de arriba) y también se concluye con la forma A C.
Al considerar ambos tipos de conclusiones, el nº de silogismos asciende a 512. Los resultados mostraron el efecto de la figura 4 y 1. Ello significa que muchos (71%) daban una conclusión A-C (figura 4) y otro tanto, daba la conclusión de C-A (figura 1).
Las conclusiones A—C se ajustan a un cambio de orden de las premisas y a un posible cambio de término medio. En el caso de figura 4, donde A-C es la conclusión, lo que se hace mentalmente es invertir el orden de las premisas y así la figura 4 se convierte en figura 1.

Los trabajos experimentales sobre el silogismo categórico se centran en el cómo influyen los aspectos estructurales y de contenido en el rendimiento de los sujetos. El rendimiento de los sujetos ha sido variable, desde 89% de respuestas correctas hasta un 8%.
2.1. La hipótesis de la atmósfera de las premisas
La hipótesis de la atmósfera no es una teoría, sino una explicación basada en la tendencia que se observa en los sujetos al dar sus respuestas y que parecía determinada por los aspectos estructurales del silogismo. El trabajo de Woodworth y Sell 1935, presentó una tarea en donde se debía evaluar la validez de los argumentos. Encontraron que se equivocaban y que ello se explicaba por el modo de las premisas. Cuando las dos premisas eran UNIVERSALES ( A – E) afirmativa o negativa, mostraban tendencia a elegir una conclusión UNIVERSAL y cuando las dos premisas eran afirmativas (A – I) daban conclusión afirmativa. Lo llamaron “Atmósfera” pues inducía a conclusión del mismo tipo. Mas tarde en 1969, Begg y Denny explicitaron los principios del efecto teniendo en cuenta cantidad y cualidad de las premisas:
- Cuando las premisas contienen al menos una premisa particular, entonces la conclusión es particular, y en el caso contrario es universal, y
- Cuando contienen al menos una premisa negativa, entonces la conclusión es negativa, y en el caso contrario, afirmativa.
Lo enunciaron como “Efecto atmósfera” siendo objeto de estudio para investigaciones que querían averiguar sobre identificación y análisis de los errores.
Sells 1936, indica que puede ser debido a un principio general de prudencia por el que se supone que las conclusiones son menos prudentes que las particulares. Aún así y siendo bastante evidente el que no queramos etiquetar a todos, no ha tenido demasiada aceptación, pues parece ser que también se evidencia que aún queriendo ser prudentes, no concluimos muy frecuentemente de forma particular-negativa (O), cuando sería lo que nos decía Sells.
La tendencia no lógica del efecto atmósfera en los resultados puede predecir un porcentaje aceptable de respuestas. Sin embargo los propios autores, reconocieron luego que el efecto solo explicaba la tendencia al error, pero que no era una verdadera teoría del razonamiento. También se encontraban diferentes respuestas ante silogismos válidos y no válidos, dándose el sesgo en la respuesta. Tampoco predice los distintos niveles de dificultad de los silogismos categóricos, además de indicar que siempre se dará un conclusión, cuando los resultados indican que no siempre se da conclusión válida cuando la tarea es de producción.
2.2. Modelos basados en la interpretación de las premisas
Chapman y Chapman 1959, señalaban que el efecto atmósfera podía se más una ilusión de irracionalidad pues ellos explicaban los resultados de sus estudios por la conversión ilícita de las premisas y por la inferencia probabilística.
El principio de inferencia probabilística supone que mostramos una consistencia interna en nuestro razonamiento pero con reglas erróneas. Esta nos conduce a que consideremos que las entidades que comparten determinadas propiedades tendrían mayor probabilidad de compartir otras relaciones. Un ejemplo:
- Algunos A son B Algunos peces son carnívoros.
- Algunos C son B Algunas plantas son carnívoras
- Algunos C son A Algunos plantas son peces
La conclusión relaciona C con A apoyándose en B (común a ambas premisas), y por lo tanto hará probable que C y A se encuentren relacionados.
Si le damos contenido vemos que la conclusión no se sigue necesariamente de las premisas.
La hipótesis sobre la conversión ilícita es un error en la interpretación de la Universal afirmativa y de la particular negativa, sin aludir al efecto atmósfera y sin hacer referencia a una regla de inferencia falsa. El error ocurre cuando se interpreta que la premisa Universal afirmativa A, “Todos los A son B” es equivalente a “Todos los B son A”; y que la premisa Particular negativa O “Algunos A no son B” es equivalente a “Algunos B no son A”, pero sí es lícita para las premisas en universal negativa y particular positiva (E – I):
- (A): Todos los hombres son seres mortales - no es equivalente a: Todos los seres mortales son hombres.
- (E): Ningún hombre es un ser inmortal - equivale a: Ningún ser inmortal es un hombre
- (O): Algunos hombres no son deportistas - no equivale a: Algunos deportistas son hombres
- (I): Algunos hombres son deportistas - equivale a: Algunos deportistas son hombres.
La conversión consiste en intercambiar los términos sujeto y predicado entre ambos enunciados Un aspecto importante del enunciado categórico es la distribución de sus términos. El término estará distribuido si se refiere a todos los miembros de la clase designada por dicho término:
| Tabla 4.1. Distribución de los términos de un enunciado categórico | ||
| AFIRMATIVO PREDICADO No distribuido | AFIRMATIVO PREDICADO distribuido | |
| UNIVERSAL SUJETO distribuido |
A Todos los A son B Todos los hombres son mortales (todos y cada uno de ellos) |
E Ningún A es B Ningún hombre es inmortal tanto sujeto como predicado están distribuidos porque la relación se refiere a la exclusión de hombres y de inmortales |
| PARTICULAR SUJETO no distribuido |
I Algunos A son B Algunos hombres son mortales |
O Algunos A no son B |
De esta forma la cantidad del enunciado determina que el sujeto se encuentre distribuido en los enunciados universales A – E y no en los particulares I – O; la calidad determina la distribución del término predicado. En el Universal Negativo tanto el sujeto como el predicado están distribuidos porque la relación se refiere tanto a las exclusión de todos los hombres de la clase inmortales como a la exclusión de todos los inmortales de la clase de hombres.
La afirmación negación de la inclusión de clases determina que el predicado se encuentre distribuido en los enunciados negativos E – O y que no esté en los enunciados afirmativos A -I.
El cuadro anterior ilustra por qué la conversión sólo es legítima para los E e I, pues son los únicos que tienen los mismos valores en su distribución: sujeto y predicado distribuidos en E, y no distribuidos en I, permitiendo realizar la conversión del enunciado y que con ello no se altere ni su cantidad ni su calidad.
Revlis formula una propuesta más concreta basada en la conversión de todas las premisas y en el supuesto de que se prefiere razonar con estas versiones convertidas de las premisas. Hay una primera etapa de procesamiento en la que se codifican las premisas y se convierten quedando representadas ambas versiones. Y luego, se elabora una representación compuesta de las dos premisas y se pasa a la codificación de la conclusión de modo semejante a la primera etapa. Por último hay un proceso de comparación entre la representación conjunta de las premisas y la representación de la conclusión. Si ambas con congruentes entonces se acepta el silogismo como válido. Si son incongruentes se procedería con la comparación de las representaciones en sus versiones originales sin conversión, hasta encontrar un argumento válido. Si no se obtiene éste, o se supera el límite de tiempo, se procede o con modelo para la selección aleatoria de una de las alternativas o bien con un modelo de selección de rasgos (cantidad y calidad).
El contenido temático del silogismo puede facilitar el razonamiento, por ejemplo, la conversión de Todos los gatos son felinos en Todos los felinos son gatos, daría lugar a una premisa contraria al conocimiento del sujeto. El razonamiento silogístico con contenido es mejor que el abstracto porque el contenido bloquea la conversión de las premisas en el proceso de codificación. Sin embargo, los resultados experimentales son contrarios porque el efecto del contenido o de las creencias se sigue manifestando incluso en aquellos silogismos en los que la conversión no altera la validez del argumento.
Con respecto al efecto del contenido (sesgo de creencias) ya Wilkins 1928 había encontrado que el contenido familiar facilitaba el rendimiento, pero que disminuía si el contenido entraba en conflicto con la estructura lógica. Ejemplos de argumentos válidos e inválidos con conclusiones creíbles e increibles:
| SILOGISMO | EJEMPLO | % |
| VÁLIDO CREIBLE |
Ningún perro policía es vicioso Algunos perros muy entrenados son viciosos Algunos perros muy entrenados no son perros policías |
89% |
| VÁLIDO INCREÍBLE |
Ningún producto nutritivo es barato Algunas vitaminas son baratas Algunas vitaminas no son nutritivas |
56% |
| INVÁLIDO CREIBLE |
Ningún producto aditivo es barato Algunos cigarrillos son baratos Algunos productos aditivos no son cigarrillos |
71% |
| INVÁLIDO INCREIBLE |
Ningún millonario es muy trabajador Algunas personas ricas son muy trabajadoras Algunos millonarios no son personas ricas |
10% |
En líneas generales los sujetos tienden a considerar que un argumento es válido si están de acuerdo con su conclusión y que es falso si no lo están. Además, Evans, Barston y Pollard 1983 encontraron una interacción entre validez lógica y credibilidad de las conclusiones, siendo el efecto mayor para los silogismos inválidos que para los válidos. Se obtuvo que los sujetos aceptaban más conclusiones creibles que increibles independientemente de su validez lógica. Sin embargo, la diferencia entre la aceptación de conclusiones inválidas creíbles y conclusiones inválidas increibles fue mayor que la diferencia entre conclusiones válidas creíbles.
Evans y cols propusieron dos modelos para explicar cómo se realiza el proceso de evaluación de las conclusiones:
- modelo de escrutinio selectivo y,
- modelo basado en una mala interpretación de la “necesidad lógica”.
El modelo de escrutinio selectivo sostiene que los sujetos se centran primero en la conclusión del argumento y si ésta es coherente con su sistema de creencias, la aceptan sin más. Está basada en los análisis de los protocolos verbales en los que se identificaban tres tipos de estrategias para la solución de los silogismos:
- “Estrategia solo la conclusión”: solo mencionan la conclusión.
- “Estrategia de la conclusión a las premisas”: mencionan primero la conclusión y luego las premisas.
- “Estrategia de las premisas a la conclusión”: mencionan antes las premisas.
Los sujetos de los dos primeros grupos 1 y 2, presentaron la mayor tendencia a responder de acuerdo con la credibilidad de la conclusión. Hay que tener en cuenta que no explica el modelo el efecto de la lógica sobre las propias conclusiones creíbles. Algunos autores ponen de manifiesto que los sesgos de creencias se siguen dando, en las tareas en las que los sujetos deben generar sus propias conclusiones y en las que, no hace falta un proceso de escrutinio de la conclusión.
El modelo basado en una mala interpretación del concepto de necesidad dice que los sujetos en realidad no entienden la necesidad lógica. Un argumento deductivo es válido sólo si es imposible que su conclusión sea falsa mientras que sus premisas son verdaderas.
Un silogismo con conclusiones posibles, pero no necesarias, se denomina un silogismo inválido indeterminado y cuando no se sigue ninguna conclusión se denomina silogismo inválido determinado.
|
SILOGISMO INVÁLIDO INDETERMINADO Figura 2, modelo AAA |
SILOGISMO INVÁLIDO DETERMINADO Figura 4 modelo AAE |
||
|
Todos los animales son seres vivos Todos los perros son seres vivos Todos los perros son animales |
Todos los A son B Todos los C son B Todos los C son A |
Todos los cobardes son seres vivos Todos los seres vivos son reactivos Ningún ser reactivo es cobarde |
Todos los A son B Todos los B son C Ningún C es A |
Los sujetos responden de acuerdo con la credibilidad de las conclusiones en los silogismos inválidos indeterminados, pero cuando es inválido determinado no se sigue ninguna conclusión y la credibilidad no ejerce ninguna influencia. La credibilidad surte efecto sobre los silogismos inválidos indeterminados y el efecto desaparece en los silogismos inválidos determinados. No obstante ambos modelos dejan sin explicar el proceso de razonamiento y solo se centran en los errores para algunos silogismos (inválidos indeterminados).
Begg y Harris sostienen que los errores de razonamiento silogísticos se encuentran en la interpretación de las premisas, pero no por un proceso de conversión sino por la interpretación de los cuantificadores según las convenciones lingüísticas. Los sujetos los interpretan de tres formas: Ninguno como exclusión, algunos como intersección y todos como identidad. La interpretación de “alguno” como “todos” y de “algunos no” como “ninguno” son propias del significado lógico pero son inútiles psicológicamente.
Esta explicación de los errores se centra en la interpretación de las premisas según las implicaturas conversacionales propuestas por Grice, 1975. Implicatura designa el contenido implícito de lo que decimos y la máxima conversacional de cantidad explicaría los errores en la interpretación de los cuantificadores particulares. Según la máxima de cantidad la conversación debe ser todo lo informativa que requiera el diálogo, aunque nunca más de lo necesario. Esta explicaría que los sujetos no acepten la relación de subalternancia entre un enunciado universal y uno particular: uno universal implica su enunciado subalterno correspondiente como Todos los los hombres son mortales implica que algunos hombres son mortales. Para las personas sería poco informativo decir “algunos” cuando se sabe que son “todos”. Sigue el cuadro de oposición.
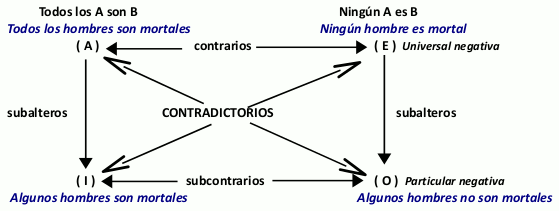
Se aprecia que tanto A como E implican sus correspondientes enunciados subalternos I y O. Ambos enunciados comparten el sujeto, el predicado y la calidad, pero difieren en la cantidad.
A y E son contrarios porque comparten el mismo sujeto y el mismo predicado pero no pueden ser ambos verdaderos, aunque pueden ser falsos.
Entre A y O, y E e I se aprecia que son contradictorios pues tienen el mismo sujeto y el mismo predicado, pero difieren en calidad y cantidad. Uno de ellos es la negación del otro, ambos no pueden ser verdaderos o falsos a la vez.
La máxima conversacional de cantidad dice que debe transmitir la mayor cantidad de información posible y no ocultar deliberadamente parte de la información. El significado lógico de “algunos” sería una transgresión de las máximas conversacionales cuando se sabe que “todo” también es verdadero y este último cuantificador es que transmite mayor información.
Begg 1987, Newstead 1989 y Politzer 1986-1990 ponen de manifiesto que la interpretación de algunos cuantificadores se rige por las implicaturas conversacionales y no por la lógica. Defienden la racionalidad desde un modelo de convenciones lingüísticas en el que las reglas otorgan una lógica intuitiva o natural, pero no hay datos experimentales suficientes como decir que las interpretaciones “Griceanas” constituyan la principal fuente de errores del razonamiento silogístico.
Los modelos de conversión también han sido criticados. Estos modelos explican el efecto atmósfera bajo el supuesto racionalista de que el razonamiento es lógicamente correcto, pero con unas representaciones invertidas de las premisas y no consideran la figura. Sin embargo, Frase y Pezzoli y Frase 1968, encontraron un efecto análogo al efecto atmósfera con la figura del silogismo. El tipo de figura también presentaba diferentes grados de dificultad, siendo la cuarta más fácil que la primera. Johnson- Laird y Steedman 1978 , decían que cuando los sujetos tenían que producir la conclusión del argumento, éstos generaban conclusiones A-C (donde la premisa mayor se correspondía con el sujeto y predicado en la menor) con la figura 4, y C-A con la figura 1.
2.3. Modelos basados en la representación de conjuntos
El método de Euler se basa en la utilización de círculos para la representación en un plano de las relaciones entre los conjuntos comprendidos en las premisas del argumento.
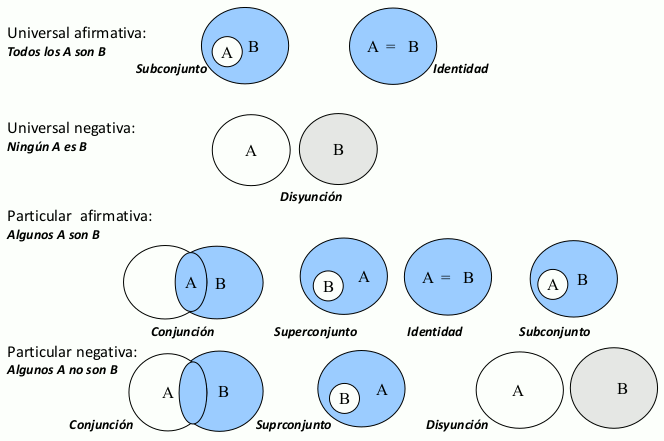
Un argumento es válido cuando la conclusión es verdadera en todos los diagramas que representan todas las posibles combinaciones de las dos premisas. Es un proceso bastante costoso, sobre todo porque el número de combinaciones posibles es generalmente mayor que el producto de los diagramas de las dos premisas al existir más de una forma de combinarlos.
Erickson 1974, 1978 propuso una teoría del razonamiento silogístico basada en los círculos de Euler. Los sujetos representaban cada premisa de forma análoga a la representación espacial de los círculos. Las distintas interpretaciones posibles de las premisas llevan asociados unos parámetros probabilísticos que determinan una selección.
- En la primera etapa también influirá el contenido del argumento. Para evaluar o producir una conclusión se combinan las representaciones de las premisas en una sola representación del silogismo.
- Etapa de combinación: se asume que no hace el sujeto análisis exhaustivo de todas las combinaciones posibles de las interpretaciones de las premisas, sino que selecciona una combinación de acuerdo con los parámetros probabilísticos.
- En esta etapa se selecciona etiqueta verbal que se corresponda con la descripción de la combinación obtenida para dar la respuesta.
Los errores en el proceso pueden ocurrir en cualquiera de las etapas y se asume que los sujetos son proclives al efecto atmósfera. El problema principal es el número tan grande de formas distintas en las que se pueden combinar los diagramas.
El modelo de la cadena transitiva de Guyote y Sternberg 1981, asume una representación simbólica semejante a los círculos de Euler, pero libre de errores al ser una representación exhaustiva. El peso del modelo es la especificación de los procesos de combinación y comparación de la interpretaciones de las premisas:
- En el proceso de combinación, las interpretaciones de las premisas se van integrando en “cadenas transitivas”, que son los enlaces entre el primer y último término de las premisas a través del término medio. Se pueden producir errores por la capacidad limitada de la memoria de trabajo.
- En la etapa de comparación, se elige una conclusión concordante con las representaciones combinadas y se da la respuesta que se corresponda con la conclusión seleccionada. Los errores pueden ser debidos a falta de considerar alguna conclusión concordante con la combinación y por el efecto atmósfera.
Una de las críticas más importantes al modelo es que asume que no hay errores en la primera etapa de la representación de las premisas cuando has datos que lo cuestionan. Tampoco contemplan los efectos de la figura y se recurre al efecto atmósfera como un sesgo de respuesta sin explicación psicológica.
Los modelos basados en los círculos de Euler predicen que la dificultad dependerá del no de diagramas necesarios para la interpretación y combinación de las premisas, pero los datos ponen de manifiesto que algunos de los silogismos fáciles han podido resolverse sin dificultad con muchos diagramas y otros que son más difíciles y precisan de menos.
Newell 1981, propone otra aproximación para explicar el razonamiento silogístico por medio de la representación espacial de los diagramas de Venn. En este método se representa el silogismos en un solo diagrama. Estos utilizan círculos que se encuentran sobrepuestos de forma que representen las relaciones entre los conjuntos del silogismo. Se sombrea aquella zona en la que no hay miembros y se representa con una X las áreas en las que existe al menos un elemento cuando el enunciado categórico es particular (afirmativo o negativo).
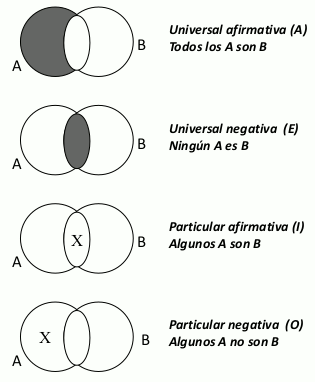
Veamos un silogismo válido EAE:
- Ningún B es A
- Todos los C son B
- Ningún C es A
donde se representan con los diagramas de Venn los tres términos del silogismo A, B y C, exponiéndose el espacio o universo del discurso. Las áreas sombreadas son las vacías, donde no hay miembros de la relación expresada por los dos conjuntos según premisa. Se sombreará la parte vacía del universo del discurso donde no haya elementos.
Según Newell ,este modelo pretende acomodar los silogismos categóricos al marco general que diseñaron Newell y Simon para la solución de problemas. Se entiende que el razonamiento silogístico es un proceso de búsqueda a través del espacio del problema y que este espacio se representa de forma análoga a los diagramas de Venn. No se hacen predicciones sobre los errores, ni se aportan datos empíricos que apoyen la viabilidad del modelo (Simon 1989), comentó que es probable que la utilización sólo ocurra en sujetos expertos y que una representación en la línea de los modelos mentales es preferible, y más acorde con una aproximación del razonamiento silogístico.
Los modelos mentales de conjuntos fue una teoría del razonamiento silogístico en sus orígenes y hoy constituye un marco teórico general del razonamiento deductivo. Este comprende tres etapas:
- etapa de interpretación y representación inicial de las premisas: utiliza su conocimiento sobre el lenguaje y su conocimiento gral para comprender las premisas.
- El sujeto combina las representaciones anteriores para generar una descripción lo más sencilla posible de los modelos construidos a partir de las premisas. Debe enunciar algo que no se encuentre explícito en las premisas y es la conclusión tentativa del argumento.
- El sujeto busca modelos alternativos para poder falsar la conclusión tentativa. Si no los encuentra la conclusión es válida, pero si los encuentra, regresa a la segunda etapa para seguir probando conclusiones tentativas con contraejemplos.
En la tercera etapa se ubica el “aspecto” deductivo del razonamiento. La dificultad se explica en términos de la cantidad de procesamientoo y los errores vienen explicados por las limitaciones de la memoria de trabajo.
El principio de economía propuesto por la teoría asume que el modelo mental inicial sólo representará la cantidad de información explícita que sea necesaria para la interpretación de la premisa. Está constituido por símbolos que representan miembros representativos del conjunto.
En la universal afirmativa Todos los A son B -> “a” es un miembro representativo del conjunto A y “b” del conjunto B. Cuando un miembro del conjunto se encuentra representado dentro de un corchete [a], quiere decir que el conjunto de miembros se encuentra exhaustivamente representado. Por ejemplo si no hay miembros de “a” que no sean de “b”
[a] b
...
“b” se representa así pues no sabemos si alguno de sus miembros puede pertenecer a A.
Una sola representación del modelo mental de la universal afirmativa comprende las dos representaciones espaciales de los círculos de Euler: relación de identidad y subconjunto. Los tres puntos (...) indican que podría haber otra clase de miembros que no se encuentran representados en el modelo inicial, es como una anotación mental que indica la existencia de otros modelos que están implícitos. Pueden hacerse explícitos en la que sea necesario ampliar la información enunciada en las premisas. Por ejemplo en la representación de los miembros que no son “a” y son “b” ( ¬a b )
En la segunda etapa del modelo se deben combinar los modelos mentales de las premisas en una sola descripción. Se añade el modelo mental de la segunda premisa al modelo de la primera mediante el término medio. Si fuera una universal afirmativa: Todos los B son C, sería:
[b] c
[b] c
...
y por la combinación de ambos modelos se obtendría:
|
[ [a] b] c [ [a] b] c ... |
Todos los A son C y Algunos C son A |
los miembros de “a” se representan exhaustivamente con respecto a “b” y los miembros “b” se representan exhaustivamente con respecto a “c”. La conclusión entre “a” y “c” es Todos los A son C y Algunos C son A. En este silogismo no se puede generar otra combinación que dé otra conclusión que pueda falsar la conclusión tentativa y se concluye como válido. Este silogismo AA solamente requiere un modelo mental y es el silogismo más fácil de resolver. Repetimos, que la combinación de los modelos mentales de las premisas se complica cuando hay más modelos mentales alternativos.
|
FIGURA 3 conclusión C- A Todos los B son A (A) Ningún B es C (E ) [b] a [b] a ... |
FIGURA 3 conclusión A – C Ningún B es C (E ) Todos los B son A (A) [b] [b] c c |
|
combinando ambos modelos: [a [b] ] [a [b] ] [c] [c] ... |
|
El modelo sugiere la conclusión: Ningún C es A sin embargo, como “a” no se encuentra exhaustivamente representado y podía haber algún “c” que fuera “a” , aunque no fuera “b”, podemos generar este segundo modelo mental donde:
[a [b] ]
[a [b] ]
a [c]
[c]
...
y si este segundo modelo refuta la conclusión anterior y sugiere que “Algunos C no son A”
[a [b] ]
[a [b] ]
a [c]
a [c]
...
La teoría de los modelos mentales explica la dificultad de los silogismos y los errores por el número de modelos mentales y por el tipo de figura. Los resultados han puesto de manifiesto que cuanto mayor sea el no de modelos mentales necesarios para encontrar una conclusión válida tanto más difícil será el problema y mayor la probabilidad de error. La figura también determina la dificultad y la probabilidad de que una conclusión sea del tipo C-A o A-C. Se debe a que las conclusiones se leen en el modelo mental en la misma dirección enn la que se han representado.
Cuando no se encuentran en la misma dirección hace falta una operación que invierte el orden y/o la relación espacial entre los términos para poder realizar la combinación de los modelos mentales.
| NIVEL DE DIFICULTAD | OPERACIONES NECESARIAS PARA LA COMBINACIÓN DE LOS MODELOS MENTALES |
|
FIGURA 4 (más fácil) A B B C |
No requiere ninguna operación dado que se lee directamente la conclusión A C |
|
FIGURA 1 B A C B |
Requiere una operación de inversión del orden de las premisas |
|
FIGURA 2 A B C B |
Requiere operación de inversión de la relación espacial entre los términos de la segunda premisa |
|
FIGURA 3 (más difícil) B A B C |
Requiere una operación de inversión de la relación espacial entre los términos de la segunda premisa y cambiar el orden de las premisas o la inversión de la relación espacial entre los términos de la primera premisa |
El contenido o las creencias se consideran una fuente error pues pueden influir en la interpretación, en la combinación de modelos y en el proceso de aceptación o rechazo de la conclusión tentativa. Cuando el contenido influye puede acortar el proceso de búsqueda de modelos alternativos si la conclusión tentativa es compatible con el sistema de creencias, aunque sea inválida.
Podría ocurrir que el sujeto buscara afanosamente más modelos mentales alternativos cuando la conclusión fuera contraria a su sistema de creencias. Este efecto estaría influyendo en la búsqueda de contraejemplos. Incluso este contenido influye en los silogismos de un solo modelo mental y proponen que una conclusión increíble también podría actuar de filtro en el proceso de evaluación, haciendo que la sustituyan por una conclusión creíble o que respondan que no hay conclusión.
La teoría de los modelos mentales se basa en un procedimiento formal para la representación semántica de los operadores lógicos que unen los contenidos expresados en las premisas. La crítica fundamental se centra en que esta teoría se autodefine como semántica, pero no explica cómo se vincula el conocimiento almacenado con la construcción de los MM en la memoria de trabajo.
No determina cómo se construyen los MM, ni el orden en la construcción de la secuencia de posibles interpretaciones, ni se compromete con el tipo de representación de los MM, ni con el orden de la combinación de los MM.